Præcision er et udtryk for en riffels evne til at ramme, hvor skytten ønsker den skal ramme. Spredning er alene et udtryk for hvor meget skuddene spredes. Forskellen på disse to begreber er altså, at god præcision forudsætter både lille spredning og korrekt justerede sigtemidler. I denne artikel er spredningen den egentlige genstand for vor interesse.
Spredning måles direkte på skudhullerne i skiven – centrum til centrum. Normalt måles spredningen på tre- eller fem-skudsgrupper og typisk på en skudafstand af 100 meter (eller på 100 yards, hvis man er til engelske enheder). Et mere universelt anvendeligt mål for spredning er et gradmål – typisk opgivet i gradminutter, altså 1/60 grad. I international litteratur støder man oftest på den engelske forkortelse for gradminut: M.O.A. (Minute of angle). 1 M.O.A. svarer på 100 meter til cirka 2.5 centimeter.
Størrelsen på skudgrupper i en serie følger en normalfordelingskurve, såfremt der ikke under skydningen opstår fejl på udstyret eller ændringer i skyttens praksis. Den amerikanske ballistiker Denton Bramwell har gennemanalyseret statistikken omkring skudgrupper, hvilket har kastet en række konkrete resultater af sig.
Eftersom vurdering af spredning altid hviler på statistik, bliver vurderingen aldrig bedre end det statistiske grundlag. En enkelt skudgruppe siger groft sagt ingenting – jo flere skudgrupper der skydes, desto klarere bliver billedet af den reelle spredning. Hvis man skyder tre fem-skudsgrupper og beregner den gennemsnitlige spredning på det grundlag, vil resultatet med 95% sandsynlighed give et korrekt billede +/- 25%. Vil man ned på den halve usikkerhed, skal man basere sine beregninger på 12 fem-skudsgrupper.
Hvis en ”normal” spredning defineres til at være en spredning, der holder sig indenfor 95% af de forekommende spredninger, så vil det være helt normalt at opleve f.eks. fem-skudsgrupper med en spredning på mellem 58 % og 147% af gennemsnitsspredningen. Eller med andre ord: Med en riffel, der i gennemsnit spreder 2 cm, vil det være helt forventeligt at opleve fem-skudsgrupper på mellem godt 1 og små 3 cm og skytten vil ikke have nogen som helst indflydelse på, om en given fem-skudsgruppe falder ud i den høje eller den lave ende af spektret. For tre-skudsgrupper ligger normalområdet på 43% til 165% af gennemsnitsspredningen.
 |
 |
 |
Eksempel: En riffel, der laver gennemsnitlige 3-skudsgrupper på 3 cm (midten), kan lave grupper så små som 1,29 cm (til venstre) og så store som 4,95 cm (til højre), uden at det er tegn på noget unormalt. Skytten kan på ingen måde forhindre den store gruppe og han har ikke været specielt dygtig, når den lille gruppe dukker op.
Som det ovenfor antydes, er antallet af skud i grupperne meget væsentligt. Således kan man ikke direkte sammenligne f.eks. tre-skudsgrupper med fem-skudsgrupper, idet sidstnævnte altid vil have en større gennemsnitsstørrelse end førstnævnte. I konkrete tal er gennemsnitsspredningen for fem-skudsgrupper 27% større end for tre-skudsgrupper.
Det har naturligvis altafgørende betydning for måleresultaterne, at de indsamles under samme forhold. Mange vil mene, at det for en jagtriffel først og fremmest er egenspredningen fra et koldt løb, der er interessant og at man derfor bør lade løbet køle helt af mellem hvert skud, når man laver sine skudgrupper. Andre interesserer sig for riflens evne til at holde skuddene samlede i hurtige skudserier. Begge dele kan have sin berettigelse, blot man husker, at skudgrupper kun kan sammenlignes, hvis de er lavet under præcis de samme omstændigheder.
Bidrag til spredningen
Hvad får en given kombination af skytte, riffel og ydre omstændigheder til at holde skuddene samlet? Det korte – og en anelse banale – svar er, at så længe projektilerne sendes af sted under samme forhold med samme fart og orientering, så rammer de i samme hul. Det store problem er så at komme så tæt på denne ideelle situation, som teknisk muligt.
På praktisk jagt spiller utroligt mange faktorer ind på riflens præcision: For at føre en meningsfyldt diskussion om emnet er det derfor nødvendigt at foretage en sondring. Man kan dele faktorerne, der har indflydelse på den reelle præcision, op i tre hovedgrupper: våbnet, skytten og ydre faktorer – såsom vind og vejr
For våbnets vedkommende giver en masse forskellige fejlkilder ophav til en egenspredning.

Skyttens indflydelse på den reelle præcision er et spørgsmål om skydeteknik og i reglen er netop skytten hovedbidragsyderen til den samlede spredning. I relation til skyttens betydning er våbnets brugerflade, som omfatter aftræk, sigte samt riflens ergonomi og balance, interessant, fordi disse ting har meget at sige i forhold til skyttens muligheder for at udnytte riflen præcisionspotentiale maximalt.
Sidstnævnte ydre faktorer kan også have stor indflydelse på den præcision man oplever på praktisk jagt.
I arbejdet med spredning er det interessant at vide, hvordan den samlede spredning påvirkes af de enkelte kilder til spredning. Holder vi fast i den simple inddeling i tre hovedgrupper – våben, skytte og ydre forhold – og forstiller vi os at vi kunne isolere de tre spredningsbidrag således at vi nøjagtigt vidste hvor meget våbnet i sig selv spreder, hvor meget skytten i sig selv spreder og hvilken spredning de ydre forhold i sig selv forårsager, så kunne man fristes til at tro, at den samlede spredning simpelt findes ved at lægge de tre bidrag sammen. Sådan er det ikke.
Den korrekte statistiske formel for den samlede gennemsnitlige spredning er derimod kvadratroden af summen af delspredningernes kvadrat. Eller matematisk udtrykt:
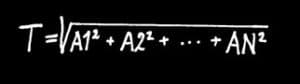
Hvor T er den samlede spredning, A1 er delspredning 1, A2 er delspredning 2 osv. osv.
I dette tilfælde har vi tre delspredninger og regnestykket ser således ud:
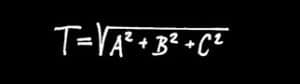
T er den samlede spredning, A er riflens egenspredning, B er skyttens spredning og C er spredningen forårsaget af ydre forhold.
Forholdet mellem spredningskilderne
Vi kan med afsæt i ovenstående formel se lidt nærmere på forholdet mellem kilderne til riflens spredning. Lad os antage en situation, hvor ydre forholds bidrag til spredning er så småt, at det kan negligeres – hvilket ofte er tilfældet i relation til praktisk jagt på moderate skudhold – og se på forholdet mellem våbnets og skyttens bidrag til spredningen.
 |
 |
 |
Eksempel: Riflen har en egenspredning på 3 cm (til venstre), skytten spreder isoleret set over 7 cm (midten). Den resulterende samlede spredning er på 7,6 cm (til højre). Riflens egenspredning har dermed ikke haft den store indflydelse på den samlede spredning – det er skyttens bidrag der for alvor spreder skuddene, fordi skyttens rystelser er langt større end riflens egenspredning.
En opspændt riffel præsterer med et givent sigte og en given ammunition fem-skudsgrupper med en gennemsnitlig størrelse på 3 cm. Lad os antage, at en given skytte i en laser-skydesimulator tilsvarende præsterer “fem-skudsgrupper” fra en skydestok på 7 cm. Den samlede gennemsnitlige spredning under virkelige forhold kan i så tilfælde beregnes til kvadratroden af (7*7 + 3*3) – altså kvadratroden af 58, som er 7,6 cm. Den samlede spredning er altså i dette tilfælde kun 0,6 cm større end skyttens spredning, på trods af, at riflens egenspredning var 3 cm.
Ser vi på en lidt dårligere riffel, der laver fem-skudsgrupper med en gennemsnitlig størrelse på 5 cm, vil den samme skytte præstere en samlet spredning på 8,6 cm, altså blot 1 cm mere, end hvis riflen i sig selv var langt mere præcis med en egenspredning på 3 cm.

På praktisk jagt betyder riflens egenspredning altså ikke så meget som mange tror. Kun hvis skytten forstår at finde et klippefast anlæg, kan en fin egenspredning reelt udnyttes. Kan skyttens egenspredning således reduceres til 3 cm, bliver den samlede spredning henholdsvis 4,2 cm for riflen med egenspredning på 3 cm og 5,8 cm for riflen med egenspredning på 5 cm.
Går vi helt i den anden grøft og ser på en drivjagtsriffel, der skal anvendes fritstående mod bevægeligt mål, vil kun trænede skytter kunne præstere en samling på 15 cm på 100 meter. Den samlede spredning på rifler med egenspredninger på henholdsvis 3, 5 og 10 cm, bliver i dette tilfælde: 15,3 cm (egenspredning 3 cm), 15,8 cm (egenspredning 5 cm) og 18,0 cm (egenspredning 10 cm). Riflens egenspredning har således ikke overvældende indflydelse på den samlede præcision, når først skytten for alvor begynder at sprede skuddene.
Altså: Jo dårligere skytte, desto mindre betydning har riflens egenspredning. Meget få skytter er i stand til at udnytte moderne riflers præcisionspotentiale og de få, der kan, kan kun, når det sker fra meget stabile skydestillinger (hvilket sjældent forekommer på praktisk jagt).
For den praktiske riffeljæger er de tekniske detaljer omkring riflers egenspredning derfor primært af rent teoretisk interesse, medmindre man ynder at skyde med fast anlæg på meget lange skudhold. Dog må man ikke glemme, at god præcision i en riffel er udtryk for god kvalitet og at god præcision uanset skyttens formåen altid er en fordel, selvom fordelen måske er marginal.
Helt tilsvarende matematiske regler gælder for alle de forskellige fejlkilder, der tilsammen resulterer i en spredning. Det kunne f.eks. for våbnets vedkommende være fejl i kikkerten, vibrationer i piben, fejl på projektiler etc. Det betyder, at effekten af at eliminere en fejlkilde ofte ikke ret stor og dette faktum vanskeliggør i høj grad målrettede forbedringer. Man ser kort og godt ikke den store effekt af væsentlige forbedringer før antallet af fejlkilder er kraftigt reduceret.
Det er enkelt at fastslå egenspredningen
En anden konsekvens af ovenstående forhold er, at man rent faktisk kan vurdere en riffels egenspredning ganske præcist ved simpel anvendelse af en sigtekikkert med stor forstørrelsesgrad og et godt fast anlæg i form af sandsække under både for- og bagskæfte, når der prøveskydes. Under så stabile forhold kan skyttens spredning af skuddene let reduceres til 5 mm eller mindre, og det betyder, at en riffel med en reel egenspredning på f.eks. 20 mm vil præstere en gennemsnitlig fem-skudsgruppe på 20,6 mm – altså blot 0,6 mm større end riflens isolerede egenspredning svarende til en afvigelse på kun 3%. I praksis er det altså helt unødvendigt med komplicerede opspændingsanordninger, når riflers egenspredning skal anslås.
Kender man først riflens egenspredning er det kun et spørgsmål om matematik at fastslå en given skyttes spredning med pågældende riffel i forskellige stillinger.
Skyttens spredning (B), når riflens egenspredning (A) og den samlede spredning (T) er kendt udregnes efter formlen:

Eksempel (der ses fortsat bort fra vind og vejr): En riffel har en gennemsnitlig egenspredning for fem-skudsgrupper på 3,5 cm. En skytte skyder fritstående fem-skudsgrupper på gennemsnitligt 14 cm med riflen.Skyttens bidrag til den samlede spredning er jvf. formlen kvadratroden af (14*14 – 3,5*3,5) – altså kvadratroden af 183,75 som er 13,6 cm.
På den måde kan man få et krystalklart billede af en given skyttes præcision fra forskellige skydestillinger, med forskellige former for anlæg osv.
FAKTA
SKUDGRUPPENS ANATOMI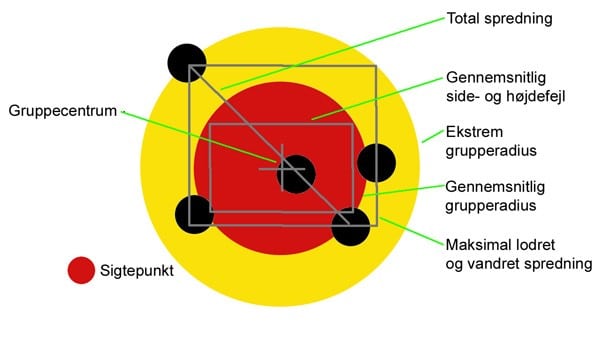 Den totale spredning måles fra centrum til centrum mellem de to skudhuller, der er længst fra hinanden. Dette er det mest almindelige sammenligningsgrundlag for skudgruppers størrelse. Målet er let at tage, men tager kun højde for to skud ud af gruppen. Den gennemsnitlige grupperadius er et udtryk for skudhullernes gennemsnitlige afstand fra gruppens centrum. Dette mål tager alle skud med i betragtning og giver dermed et klarere billede af hvad man kan forvente sig af riflen, eftersom flyvere ikke vægtes så tungt, som i den totale spredning. Den ekstreme grupperadius er et udtryk for det dårligste skud afstand fra gruppens centrum. Dette er som den totale spredning en dårlig målestok for riflens evne til et ramme. Den maksimale lodrette og vandrette spredning er et udtryk for de dårligste skuds placering i vandret og lodret plan. Målet er let at tage og bruges først og fremmest til indikation af mekaniske problemer. Hvis et af målene er mere end tre gange så stort som det andet, er det et tegn på ”ugler i mosen”. Den gennemsnitlige side- og højdefejl er et udtryk for gruppens gennemsnitlige spredning i vandret og lodret plan. Et betydeligt bedre redskab til diagnosticering af mekaniske problemer end den maksimale lodrette og vandrette spredning, eftersom alle skud – og ikke blot de dårligste – indgår ligeligt i resultatet. Sigtepunktet falder for en indskudt riffel sammen med gruppens centrum. I ovenstående eksempel er riflen altså ikke ordentligt indskudt. |
Artiklen er oprindeligt bragt i marts 2017